In my latest works I used warped FBM noise as a tools.
Here, in this #tezos4tezos drop, is used directly to generate the token.
The results resemble natural phenomena as turbulence, fluid mixing, erosion.
Erosion
Boids
Boids is a Generative Token that represent the flocking of birds over a landscape. The name ‘Boids’ comes from a famous computer animation / simulation program.
The landscape is rendered as a surface using a kind of warped noise as height map. A noise of the same kind is used as texture for the sky.
The boids are disposed along the flow lines obtained from the noise gradient. This gives the sensation that the Boids follow the undulations of the landscape.
It is possible to save a 1600×1600 png with key ‘s’.
If the token has the feature EsterEgg = True then other keys are activated:
- ‘2’ to visualize the 2D version of the token (then ‘s’ to save the png of 2D version)
- ‘3’ to visualize the 3D version of the token (then ‘s’ to save the png of 3D version)
Sources of variations are:
- Noise warping control parameters generating different grade of complexity and different shape an the landscape and Boids flock (combined on a single number on the features).
- 21 color mapping for landscape and Boids.
- Two method of surface rendering for the landscape, wireframe and blocks.
- Two possible resolution for surface rendering.
Features:
Palette: color palette name (21 different palettes)
SurfaceRendering: surface can be rendered as wireframe or as a grid of blocks
SurfaceResolution: both wireframe and blocks can be at different resolution (Low, High)
NoiseControl: noise control parameter (0 – 15)
Border: the border can be in solid color or negative color (Solid, Negative)
EsterEgg: with 20% of probability a 2D version of the same token can be visualized and saved
https://www.fxhash.xyz/generative/11369
Everything flows
The Generative Token is obtained in two stages: in the first stage warped noise is generated using the method explained by Inigo Quilez (see Licence.txt for reference); in the second stage, using Sobel method for edge detection, the noise gradient orientation is used to generate flow lines.
The first stage generate an image colored using the values of warped noise.
The second stage generate another image using gradient orientations both for shapes (the flow lines) and for coloring.
The two images are blended together to obtain the final result.
In both stages the color-maps are generated using a sinusoidal function of the gradient orientation angle with a random phases. There are 52 possible combinations of random phases.
Some palette used in the second stage are re-mixed using simplex noise with 20% of probability.
The user can save a 1200×1200 png with ‘s’.
Sources of variations are:
- Four noise warping control parameters generating different grade of complexity and different shape (combined on a single number on the features)
- 38 generated color mapping for warped noise
- 38 generated color mapping for flow lines
- Blending of the two intermediate images
Features:
Grays: 25% of probability to have a grays palette, (True, False)
Color Palette: one of the 38 possible combinations of random phases
Color Mixing: 20% of probabilty to have a re-mixed palette
NoiseControl: noise control parameter, (0 – 15)
Rare: when Grays = True and NoiseControl < 4
Variations on Tribble Fur
The Generative Token is obtained in two stages: in the first stage warped noise is generated using the method explained by Inigo Quilez (see Licence.txt for reference); in the second stage, using Sobel method for edge detection, the noise gradient orientation is used to generate flow lines for the “Fur”.
The first stage generate an image colored using the values of warped noise.
The second stage generate another image using gradient orientations both for shapes (the fur) and for coloring.
The two images are blended together to obtain the final result.
In both stages color-map can be a precalculated palette or a generated one. There are four precalculated palettes read from files and many more generated with random phases.
The user can save a 1200×1200 png with ‘s’.
Sources of variations are:
– Four noise warping control parameters generating different grade of complexity and different shape
– One flattening control parameter
– Blending of the two intermediate images
– precalculated (four) or generated (many) color mapping for warped noise
– precalculated (four) or generated (many) color mapping for flow furry lines
Features:
– Color Palette: the kind of color palette used in the two stages, (Gen + Gen | Gen + Map | Map + Gen | Map + Map)
– ColorGen: the color scheme for generated palette, can be “Grays” (one) or “Colors” (many)
– ColorMap: the precalculated color palette (the name)
– NoiseControl: noise control parameter, 0 – 15
– FlatControl: flattening control parameter, 1 – 19
– Rare: when “Color Palette” = “Gen + Gen” and “ColorGen” = “Grays”, each event has 25% probability so should be 6.25%
Zaratan II
As for the first Zaratan, the Generative Token chooses between three primitives (cubes, spheres, triangle stripes) and places it along a new kind of parametric curve with parameters varying with noise() function as source of smooth motion.
New shapes are added layer after layer with new forms and colors.
At any time the user can pause the generation by pressing ‘p’, resume it with ‘r’ and save a 1600×1600 png with ‘s’.
Sources of variations are:
– primitives choice (3)
– initial conditions
– shapes evolution
– colors evolution (only 10% will be bi-chromatic)
https://www.fxhash.xyz/generative/9659
Zaratan
Generative Token on fx(hash) Project #8343
The Generative Token chooses between three primitives (cubes, spheres, triangle stripes) and places it along a parametric curve with parameters varying with noise() function as source of smooth motion.
New shapes are added layer after layer with new forms and colors.
At any time the user can pause the generation by pressing ‘p’, resume it with ‘r’ and save a 1600×1600 png with ‘s’.
Sources of variations are:
– primitives choice (3)
– orientation (0, 90, 180, 270 degrees)
– initial conditions
– shapes evolution
– colors evolution (only 10% will be bi-chromatic)
https://www.fxhash.xyz/generative/8343
Spherical Harmonics Insectarium
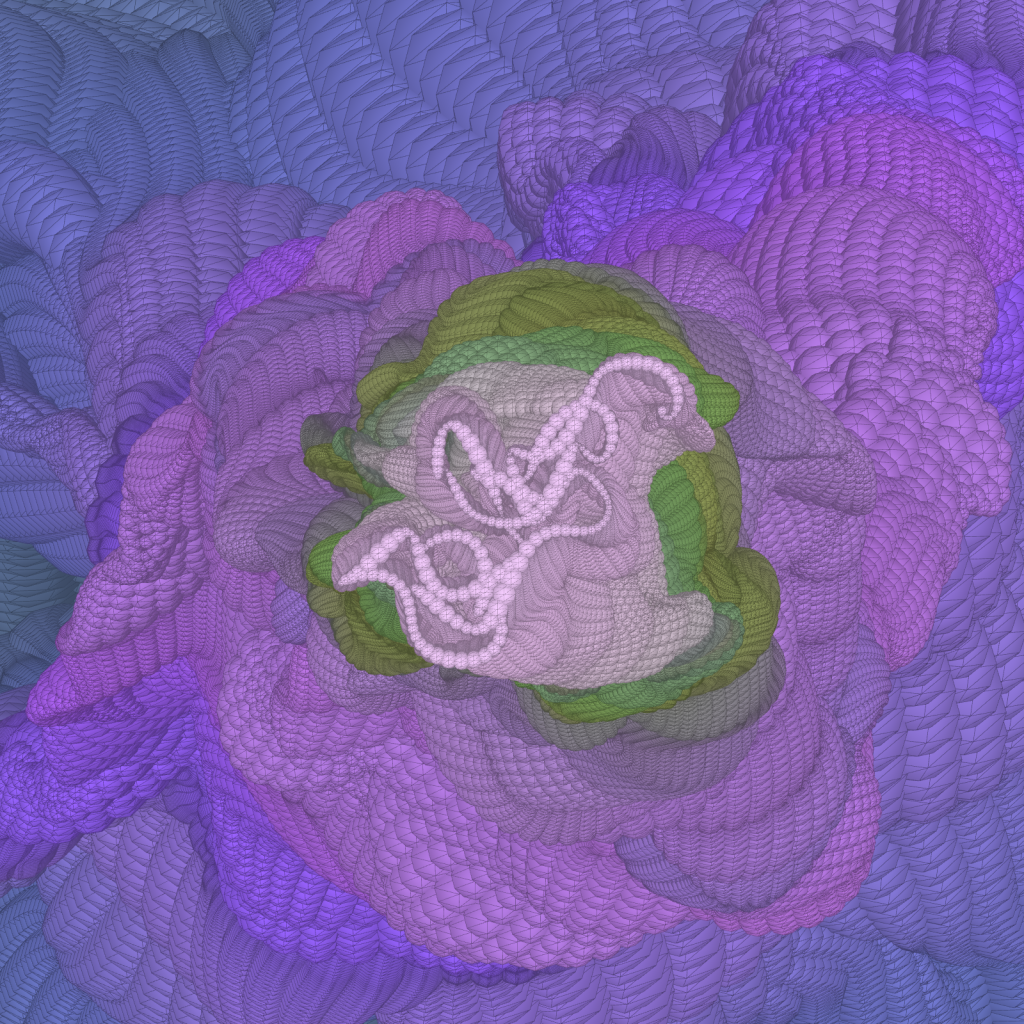
Generative Token on fx(hash) Project #7335
Spherical harmonics rendered as a surface using a parametric equation.
Parameters variations with random values (fxrand()) gives rise to various forms resembling living organism (biomorph).
Each minted token contains a unique set of 16 different biomorph disposed on a 4 by 4 grid.
https://www.fxhash.xyz/generative/7335
Cellular Neural Network #2
Cellular Neural Networks or Cellular Nonlinear Networks (CNN) are similar to Cellular Automata (CA): a grid of cells that evolve in time with local interactions with neighbouring cells.
Instead of a finite number of states for each cell (as for the CA) in CNN the cells can assume continuous values given from a chaotic oscillator and the local interactions are due to the coupling of oscillators in neighbouring cells.
With CNN is possible to model a number of physical systems described by Partial Differential Equations: Wave propagation, Heat Diffusion, Chemical Reaction-Diffusion and the likes.
In this case we have a Lorenz chaotic oscillator on each cell coupled with the 8 neighbouring oscillators.
The initial conditions, boundary conditions and coupling constant are chosen in such a way to obtain symmetrical patterns.
Here the CNN is rendered as a surface with a colormap from matplotlib (twilight).
The rendering is by means of a C++ program with openFrameworks toolkit.
https://objkt.com/asset/hicetnunc/639680
Cellular Neural Network #1
Cellular Neural Networks or Cellular Nonlinear Networks (CNN) are similar to Cellular Automata (CA): a grid of cells that evolve in time with local interactions with neighbouring cells.
Instead of a finite number of states for each cell (as for the CA) in CNN the cells can assume continuous values given from a chaotic oscillator and the local interactions are due to the coupling of oscillators in neighbouring cells.
With CNN is possible to model a number of physical systems described by Partial Differential Equations: Wave propagation, Heat Diffusion, Chemical Reaction-Diffusion and the likes.
In this case we have a Lorenz chaotic oscillator on each cell coupled with the 8 neighbouring oscillators.
The initial conditions, boundary conditions and coupling constant are chosen in such a way to obtain symmetrical patterns.
Colormap from matplotlib (flag).
The rendering is by means of a C++ program with openFrameworks toolkit.
https://objkt.com/asset/hicetnunc/609607
Reaction Diffusion on a Torus
Cellular Automata (CA) model for Belousov–Zhabotinsky (BZ) Reaction Diffusion system.
In BZ system non linear chemical oscillators give rise to pattern formation, large scale ordered patterns emerge from chaotic initial conditions.
The CA model gives rise to spiral waves patterns using only local interactions.
The periodic boundary conditions used in the CA gives a natural mapping on a torus.